Точная настройка математических формул | LaTeX
Мы уже обсудили большинство средств, необходимых для построения математических формул. Но есть еще некоторые тонкости, которые позволят вам создавать действительно красивые формулы, формулы, которые улучшат общий вид и читаемость книг и статей, которые вы печатаете.
8.1. Пунктуация
Общее правило таково: если после формулы следует точка, запятая, точка с запятой, двоеточие, вопросительный знак, восклицательный знак и т. д., ставьте знак препинания после символа $, если формула находится в тексте; но ставьте знаки препинания перед $$, когда отображается формула. Например,
1If $x<0$, we have shown that $$y=f(x).$$Итак, вам никогда не следует вводить что-либо вроде
1for $x = a, b$, or $c$.Это должно быть
1for $x = a$, $b$, $c$.В первом случае TeX напечатает $x = a, b$ как одну формулу, таким образом помещая тонкий пробел между запятой и b. Это пространство не будет таким же, как пространство между запятой и «c», поскольку пробелы между словами всегда больше, чем тонкие пробелы. Такое расстояние выглядит плохо, но во втором случае расстояние будет выглядеть хорошо.
Также важно, чтобы TeX никогда не разрывал строку абзаца на месте между запятой и b, потому что разрывы после запятых в формулах обычно неверны, как в уравнении $x = f(x, a)$. Таким образом, подавляется возможность разрыва строк в абзаце, что приводит к ухудшению внешнего вида верстаемого документа. Другими словами, если знак препинания лингвистически принадлежит предложению, а не формуле, оставьте его за пределами $.
8.2. Не курсивные буквы
Общие математические функции, такие как «журнал», всегда задаются латинским шрифтом. Лучший способ включить такие объекты в формулу — использовать следующие команды:
В следующих примерах используются некоторые из этих команд:
Последние две отображаемые формулы показывают, что некоторые команды рассматриваются TeX как большие операторы с ограничениями, такими как знак суммы. И нижний индекс \max не рассматривается как нижний индекс \log. Нижние и верхние индексы станут ограничениями, если они присоединены к \det, \gcd, \inf, \lim, \liminf, \limsup, \max, \min , \Pr и \sup в стиле отображения.
Если вам нужен латинский тип для часто используемой функции или оператора, которого нет в списке выше, вы можете легко определить свою собственную команду. Предположим, вы хотите определить оператор с ограничениями и назвать его \oper. Для этого необходимо включить в преамбулу следующее определение:
1\def\oper{\mathop{\rm oper}}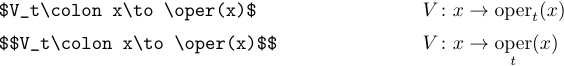
Если у вашего оператора не должно быть ограничений, используйте следующее определение:
1\def\oper{\mathop{\rm oper}\nolimits}Если вам нужен латинский тип только для одноразового использования, проще переключиться на тип \rm следующим образом:
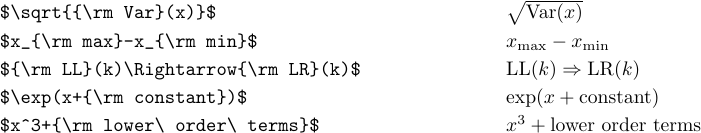
Обратите внимание на использование ‘' в последнем случае. Без них обычные пробелы были бы проигнорированы, а термины низшего порядка были бы набраны как термины низшего порядка.
Слово «мод», которое также обычно набирается в формулах латинским шрифтом, требует большей осторожности, поскольку оно используется в двух разных значениях. LaTeX предоставляет команду \bmod, которая будет использоваться, когда “mod” является бинарной операцией, и команду \pmod, которая будет использоваться, когда “mod” встречается в круглых скобках в конце формулы.
Обратите внимание, что \pmod вставляет свои круглые скобки; количество, указанное после слова «mod» в скобках, должно быть заключено в фигурные скобки, если оно не является одним символом.
Вы также можете получить другие стили шрифта так же, как и латинский шрифт, используя \rm. Например, \bf выделен жирным шрифтом:
Вы можете заметить, что символы «+» и «=" по-прежнему написаны римским шрифтом. LaTeX настроен таким образом, что команды типа \rm и \bf влияют только на прописные буквы от A до Z, строчные буквы от a до z, цифры от 0 до 9 , прописные греческие буквы от \Gamma до \Omega и математические акценты, такие как \hat и \tilde. Кстати, в этом примере не использовались фигурные скобки, поскольку $ имеет эффект группировки; \bf изменяет текущий шрифт, но это изменение является локальным, поэтому оно не влияет на шрифт, который был текущим вне формулы.
Вы также можете использовать \cal в формулах, чтобы получить заглавные буквы в «каллиграфическом» стиле.
This works only with the letters
AtoZ; you’ll get weird results if you apply\calto lowercase or Greek letters.
Также существует \mit, что означает «математический курсив». Это влияет на прописные греческие буквы.
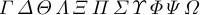
Когда действует \mit, обычные буквы от A до Z и от a до z не изменяются; они, как обычно, выделены курсивом, потому что обычно они взяты из математического курсива. И наоборот, \rm не влияет на прописные греческие буквы и математические акценты, поскольку они обычно происходят из римского шрифта.
С помощью LaTeX вы также можете ввести \it или \tt, чтобы получить текст в формуле курсивом или буквами пишущей машинки. Вы, вероятно, задаетесь вопросом, почему предусмотрены и \mit, и \it. Ответ заключается в том, что \mit — это «математический курсив» (который обычно лучше всего подходит для формул), а \it — это «текстовый курсив» (который обычно лучше всего подходит для ввода текста).
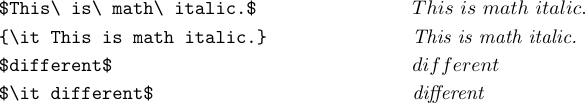
Буквы, выделенные курсивом, шире, а интервал другой. Это работает лучше в большинстве формул, но внешний вид ухудшается, когда вы пытаетесь набрать определенные слова, выделенные курсивом, например «разные» в математическом режиме. Широкий курсив «f» обычно желателен в формулах, но не в тексте. Поэтому лучше всего использовать \it в формуле, которая должна содержать настоящее слово, выделенное курсивом. Обычно это не относится к классической математике, но это обычный случай при наборе компьютерных программ:
Во втором примере показано использование коротких подчеркиваний для разделения имен идентификаторов.
8.3. Расстояние между формулами
Это распространенный случай, когда дисплей содержит более одной формулы; например, уравнение может сопровождаться дополнительным условием:
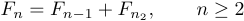
В таких случаях вам нужно указать TeX, сколько места нужно поставить после запятой, потому что обычные соглашения объединят все вместе. Чтобы получить это, вы можете ввести
1$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.Здесь \qquad означает «двойной квадрат», где «квадрат» означает некоторый объем пространства, общий для принтеров. Таким образом, \quad означает квадрат пространства принтера в горизонтальном направлении. Если вам нужен интервал, отличающийся от обычных соглашений, вы должны указать его явно, используя такие команды, как \quad и \qquad.
Раньше квад представлял собой квадратную деталь бланкового типа шириной 1 метр и высотой 1 метр - примерно размером с заглавную М; но четырехугольник LaTeX не имеет высоты.
В тексте абзаца формулы выглядят лучше, если их разделяют словами, а не только запятыми. Но если текста для вставки действительно нет, следует хотя бы оставить пробел между формулами. Сравнивать
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.и
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.которые дают
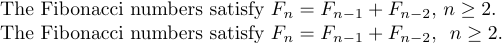
Символ ‘' здесь дает визуальное разделение, которое частично компенсирует плохой стиль.
8.4. Интервал внутри формул
Мы уже видели, что TeX автоматически распределяет математические формулы, благодаря чему в большинстве случаев они выглядят правильно. Однако естественно, что возникают исключения, поскольку количество возможных формул огромно, а правила использования пробелов в TeX довольно просты. Поэтому для таких случаев желательно иметь мелкие единицы интервала вместо больших частей, которые возникают из \ , \quad и \qquad.
Основные элементы пространства, которые TeX помещает в формулы, называются тонкими пространствами, средними пространствами и толстыми пространствами. TeX автоматически вставляет их в формулы, но вы можете добавить свой собственный интервал, когда захотите, с помощью команд
Формулы, связанные с исчислением, выглядят лучше всего, когда перед dx, dy или d вставляется дополнительный пробел; но TeX не делает этого автоматически. Следующие примеры показывают, как сообщить TeX об этих потребностях:
Обратите внимание, что во второй последней формуле после символа «/» не требовалось \,. В последнем примере также нет необходимости использовать \,, поскольку dt появляется сам по себе в числителе дроби; это визуально отделяет его от остальной части формулы.
Физические единицы, когда они появляются в формуле, должны быть записаны латинским шрифтом и отделены от предыдущего материала тонким пробелом:
Тонкие пробелы также следует вставлять после восклицательных знаков (операция факториала), если следующим символом является буква, цифра или открывающий разделитель:
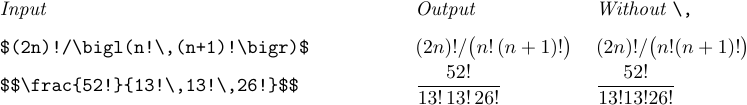
Помимо этих случаев, вы иногда будете сталкиваться с формулами, в которых символы расположены слишком плотно или в которых появляется слишком много пробелов из-за определенных неудачных комбинаций фигур. Со вкусом примененные \, или \! раскроют или сомкнут вещи, так что читатель не будет отвлекаться от математического значения формулы. Радикалы и кратные интегралы часто являются кандидатами на такую точную настройку. Вот несколько примеров ситуаций, на которые следует обратить внимание:
Правила использования интервалов TeX иногда не работают, если ‘|’ и ‘\|’ появляются в формуле, поскольку эти символы рассматриваются как обычные символы, а не как разделители. Рассмотрим формулы
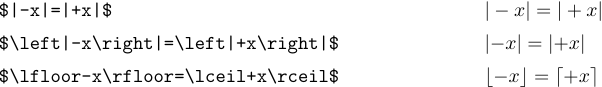
В первом случае интервал неправильный, потому что TeX думает, что знак плюс вычисляет сумму ‘|’ и ‘х’. Использование \left и \right во втором примере ставит TeX на правильный путь. Третий пример показывает, что с другими разделителями такие исправления не требуются, поскольку TeX знает, являются ли они открывающими или закрывающими.
8.5. Эллипсы
Многоточие может быть обозначено двумя разными точками, одна выше другой. Лучшие традиции различают эти две возможности. В целом правильно формулировать такие формулы, как
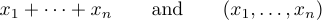
но неправильно создавать формулы типа
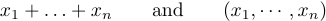
Идея состоит в том, чтобы набрать \ldots, если вам нужны три нижние точки, и \cdots, если вам нужны три вертикально центрированные точки. В общем, лучше всего использовать \cdots между + и - и знаками умножения, а также между знаками =, знаками “меньше или равно”, знаками подмножества или другими подобными отношениями. Низкие точки ставятся между запятыми, а также когда предметы соседствуют вообще без знаков между ними:
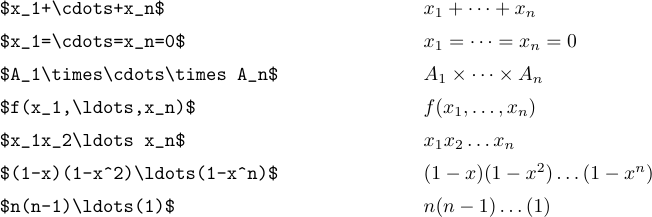Но есть особый случай, когда \ldots и \cdots не создают правильный интервал. Это происходит, когда они появляются в самом конце формулы или непосредственно перед закрывающим разделителем. В таких ситуациях необходимо дополнительное тонкое пространство. Например, рассмотрим следующие предложения:
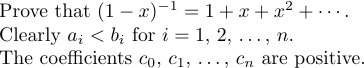
Первое предложение создается путем набора
1Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.Без \ точка была бы слишком близка к \cdots.
Второе предложение было напечатано так:
1Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.Обратите внимание на использование связей (~), которые предотвращают неправильные разрывы строк. Такие эллипсы очень распространены в некоторых формах математического письма, поэтому LaTeX предоставляет макрос \dots как сокращение для $\ldots\,$ для использования в тексте абзаца. Таким образом, третье предложение можно напечатать
1The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.8.6. Разрыв строки
Если в абзаце есть формулы, TeX, возможно, придется разбить их между строками. Он нарушит формулу только после символа отношения или после символа бинарной операции, если отношение или бинарная операция находится на внешнем уровне формулы, что означает, что она не заключена в {...}. Например, если вы наберете
1$f(x,y) = x^2-y^2 = (x+y)(x-y)$в середине абзаца есть вероятность, что TeX сломается после любого из знаков = (предпочтительно) или после - или + или - (в случае чрезвычайной ситуации). Но разрыва после запятой в любом случае не будет, так как между $ не должны стоять запятые, после которых желательны разрывы.
Если вы не хотите разрешать взлом в этом примере, кроме как после знаков =, вы можете ввести
1$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$потому что эти дополнительные фигурные скобки «замораживают» подформулы, помещая их в неразрывные коробки. Но нет необходимости беспокоиться о таких вещах, если только TeX действительно серьезно не нарушит формулу, поскольку вероятность этого довольно мала.
Если вы хотите разрешить прерывание в какой-то точке внешнего уровня формулы, вы можете сказать \allowbreak. Например, если формула
1$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$появляется в тексте абзаца, TeX позволит разбить его на две части
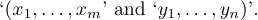
8.7. Фигурные скобки
Символы «{» и «}» используются в различных обозначениях, и LaTeX предоставляет несколько команд, которые помогут вам справиться с формулами, включающими такие вещи. Самый простой случай — когда фигурные скобки используются для обозначения набора элементов. Например, «{a, b, c}» обозначает набор из трех элементов a, b и c:
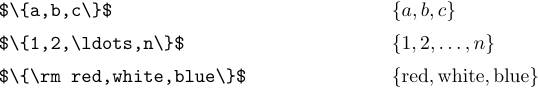
Набор также можно указать, указав общий элемент, за которым следует конкретное условие. Например, набор всех объектов x больше 5 можно записать следующим образом:
Это два варианта обозначения одного и того же набора. Первый требует использования \mid для получения вертикальной черты, а второй не требует ничего, кроме двоеточия, которое рассматривается как бинарная операция.
Когда разделители становятся больше, их следует называть \bigl, \bigm и \bigr:
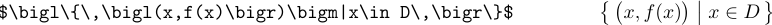
В формулах с еще большими разделителями будут использоваться команды \Big, \bigg или даже \Bigg.
Вы также можете найти другое использование фигурных скобок в отображаемых формулах. На самом деле это одна левая скобка, которая указывает на выбор между несколькими альтернативами:
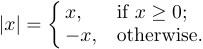
Эту конструкцию можно набрать с помощью команды \case:
1$$|x|=\case{x,&if $x\ge0$;\cr
2 -x,&otherwise.\cr}$$Каждый из случаев состоит из двух частей, разделенных символом &, который играет особую роль при построении табличных структур. Слева от & находится математическая формула, неявно заключенная в $...$; справа от & находится обычный текст. Таким образом, -x во второй строке будет набран в математическом режиме, а иначе будет набран в горизонтальном режиме. Пробелы до и после & игнорируются. Случаев может быть сколько угодно, но обычно их всего два. За каждым регистром должен следовать \cr.
Горизонтальные скобки будут установлены над или под частями отображаемой формулы, если вы используете команды \overbrace или \underbrace. Такие вещи считаются большими операторами, такими как \sum, поэтому вы можете установить ограничения выше или ниже их, указав верхние или нижние индексы:
8.8. Матрицы
Матрицы — довольно распространенные объекты в математических формулах; это просто прямоугольные массивы формул, расположенных в строках и столбцах. LaTeX предоставляет команду \matrix для работы с наиболее распространенными типами матриц.
Например, предположим, что вы хотите указать отображение
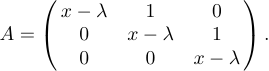
Все, что вам нужно сделать, это ввести
1$$A=\left(\matrix{x-\lambda&1&0\cr
2 0&x-\lambda&1\cr
3 0&0&x-\lambda\cr}\right).$$Это очень похоже на конструкцию \cases, которую мы рассматривали ранее; за каждой строкой матрицы следует \cr, а между отдельными элементами каждой строки используются знаки &. Однако, в отличие от \cases, вы должны размещать вокруг матрицы свои собственные разделители \left и \right. Причина в том, что в разных конструкциях матриц могут использоваться разные разделители. С другой стороны, круглые скобки используются чаще, чем другие разделители, поэтому вы можете ввести \pmatrix, если хотите, чтобы LaTeX установил для вас круглые скобки:
1$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$Каждая запись матрицы обычно центрируется в своем столбце, и каждый столбец расширяется настолько, насколько необходимо, чтобы вместить содержащиеся в нем записи, а между столбцами имеется четырехъядерное пространство. Если вы хотите, чтобы что-то вышло заподлицо слева/справа в столбце, добавьте за ним/предшествуйте ему \hfill.
Каждая запись матрицы обрабатывается отдельно от остальных и оформляется как математическая формула в текстовом стиле. Таким образом, например, если вы скажете \rm в одной записи, это не повлияет на другие. Сказать {\rm x&y} недопустимо.
Матрицы часто представляют собой общие шаблоны, в которых для обозначения пропущенных строк или столбцов используются эллипсы. Вы можете верстать такие матрицы, помещая эллипсы в отдельные строки и/или столбцы. Помимо \ldots, LaTeX предоставляет для таких конструкций \vdots (вертикальные точки) и \ddots (диагональные точки). Рассмотрим следующую матрицу
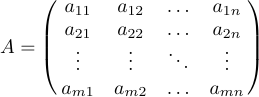
это указано как:
1$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
2 a_{21}&a_{22}&\ldots&a_{2n}\cr
3 \vdots&\vdots&\ddots&\vdots\cr
4 a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$Иногда матрица ограничена сверху и слева формулами, которые присваивают метки строкам и столбцам. Для этой ситуации в LaTeX определен специальный макрос \bordermatrix. Например, дисплей
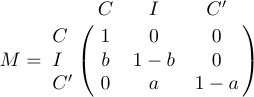
получается, когда вы вводите
1$$M=\bordermatrix{&C&I&C'\cr
2 C&1&0&0\cr
3 I&b&1-b&0\cr
4 C'&0&a&1-a\cr}$$В первой строке указаны верхние метки, которые появляются над большими левой и правой круглыми скобками; в первом столбце указаны левые метки, которые набираются заподлицо слева, непосредственно перед самой матрицей. Элемент на пересечении первого столбца и первой строки обычно пуст. И, как и \pmatrix, \bordermatrix вставляет свои собственные круглые скобки.
Размещать матрицы в тексте абзаца обычно нецелесообразно. Причина в том, что они настолько большие, что их лучше видно. Но все же иногда вы можете захотеть этим пренебречь. В этом случае вы можете использовать \choose или \atop:
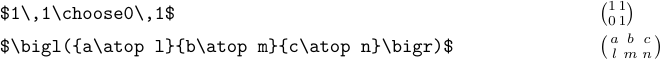
Макрос \matrix не создает такие маленькие массивы.