Тонка настройка математичних формул | Підручник з LaTeX
Ми вже обговорили більшість засобів, необхідних для побудови математичних формул. Але є ще деякі тонкощі, які дозволять вам створювати справді красиві формули, формули, які покращать загальний вигляд і читабельність книг і паперів, які ви друкуватимете.
8.1. Розділові знаки
Загальне правило таке: якщо після формули стоїть крапка, кома, крапка з комою, двокрапка, знак питання, знак оклику тощо, ставте розділові знаки після $, якщо формула є в тексті; але поставте розділовий знак перед $$, коли формула відображається. Наприклад,
1If $x<0$, we have shown that $$y=f(x).$$Отже, ви ніколи не повинні вводити нічого подібного
1for $x = a, b$, or $c$.Це повинно бути
1for $x = a$, $b$, $c$.У першому випадку TeX набере $x = a, b$ як одну формулу, таким чином ставлячи тонкий пробіл між комою та b. Цей пробіл не буде таким самим, як пробіл між комою та “c”, оскільки пробіли між словами завжди більші за тонкі пробіли. Такий інтервал виглядає погано, але в другому випадку інтервал буде виглядати добре.
Також важливо, що TeX ніколи не розриватиме рядок абзацу на проміжку між комою та b, оскільки розриви після коми у формулах зазвичай неправильні, як у рівнянні $x = f(x, a)$. Таким чином, припиняється можливість розриву рядків в абзаці, що призводить до погіршення зовнішнього вигляду набраного документа. Іншими словами, якщо розділовий знак лінгвістично належить до пропозиції, а не до формули, залиште його поза символами $.
8.2. Некурсивні літери
Звичайні математичні функції, такі як “log”, завжди встановлюються латиницею. Найкращий спосіб включити такі об’єкти у формулу – скористатися такими командами:
У наступних прикладах використовуються деякі з цих команд:
Останні дві відображені формули показують, що TeX розглядає деякі команди як великі оператори з обмеженнями, як знак підсумовування. І нижній індекс у \max не обробляється як нижній індекс у \log. Нижні та верхні індекси стануть обмеженнями, коли їх приєднано до \det, \gcd, \inf, \lim, \liminf, \limsup, \max, \min , \Pr і \sup, у стилі відображення.
Якщо вам потрібен латинський шрифт для часто використовуваних функцій або операторів, яких немає в списку вище, ви можете легко визначити власну команду. Припустімо, ви хочете визначити оператор з обмеженнями та назвати його \oper. Для цього ви повинні включити таке визначення у преамбулу:
1\def\oper{\mathop{\rm oper}}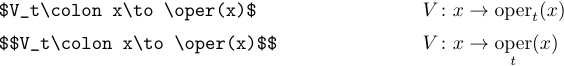
Якщо ваш оператор не повинен мати обмежень, використовуйте таке визначення:
1\def\oper{\mathop{\rm oper}\nolimits}Якщо вам потрібен римський шрифт лише для одноразового використання, простіше переключитися на тип \rm таким чином:
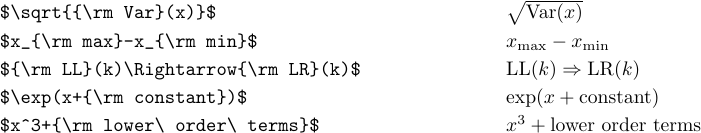
Зверніть увагу на використання ‘\ ’ в останньому випадку. Без них звичайні пробіли ігнорувалися б, а «терми нижчого порядку» були б набрані як «терми нижчого порядку».
Слово “mod”, яке також зазвичай встановлюється латиницею у формулах, потребує більшої уваги, оскільки воно використовується двома різними способами. LaTeX надає команду \bmod для використання, коли «mod» є бінарною операцією, і команду \pmod для використання, коли «mod» зустрічається в дужках у кінці формули.
Зверніть увагу, що \pmod вставляє власні дужки; кількість, яка з’являється після “mod” у цих дужках, має бути взята у дужки, якщо це не один символ.
Ви також можете отримати інші стилі шрифту так само, як ви отримуєте латинський шрифт, використовуючи \rm. Наприклад, \bf виділяє жирний шрифт:
Ви можете помітити, що «+» і «=» все ще написані латиницею. LaTeX налаштовує так, що такі команди, як \rm і \bf, впливають лише на великі літери від A до Z, малі літери від a до z, цифри від 0 до 9. , великі грецькі літери від \Gamma до \Omega, а також математичні наголоси, наприклад \hat і \tilde. До речі, у цьому прикладі фігурні дужки не використовувалися, оскільки $ мають ефект групування; \bf змінює поточний шрифт, але зміна є локальною, тому вона не впливає на шрифт, який був поточним поза формулою.
Ви також можете сказати \cal у формулах, щоб отримати великі літери в “каліграфічному” стилі.
Це працює лише з літерами від
AдоZ; ви отримаєте дивні результати, якщо застосувати\calдо малих або грецьких літер.
Є також \mit, що означає “математичний курсив”. Це впливає на грецьку мову у верхньому регістрі.
Коли \mit діє, звичайні літери A на Z і a на z не змінюються; вони виділені курсивом, як зазвичай, оскільки вони зазвичай походять від математичних курсивних шрифтів. І навпаки, \rm не впливає на великі грецькі літери та математичні наголоси, оскільки вони зазвичай походять від латинського шрифту.
За допомогою LaTeX ви також можете ввести \it або \tt, щоб отримати текст курсивом або літери друкарської машинки у вашій формулі. Ви, напевно, дивуєтеся, чому надано і \mit, і \it. Відповідь полягає в тому, що \mit — це «математичний курсив» (який зазвичай найкраще підходить для формул), а \it — це «текстовий курсив» (який зазвичай найкраще підходить для запуску тексту).
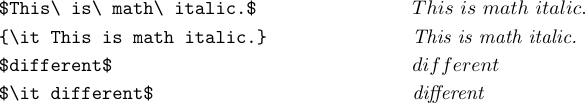
Математичні курсиви ширші, а інтервали інші. Це працює краще в більшості формул, але зовнішній вигляд страждає, коли ви намагаєтеся ввести певні слова курсивом, як-от «різні» в математичному режимі. Широкий курсив ‘f’ зазвичай бажаний у формулах, але не в тексті. Тому найкраще використовувати \it у формулі, яка має містити фактичне слово, виділене курсивом. Зазвичай це не класична математика, але це звичайний випадок, коли комп’ютерні програми набираються:
У другому прикладі показано використання коротких підкреслень для розбиття імен ідентифікаторів.
8.3. Інтервал між формулами
Це звичайний випадок, коли дисплей містить більше однієї формули; наприклад, рівняння може супроводжуватися побічною умовою:
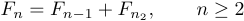
У таких випадках вам потрібно вказати TeX, скільки місця слід поставити після коми, оскільки звичайні угоди збивають речі разом. Щоб отримати це, ви можете ввести
1$$F_{n}=F_{n-1}+F_{n-2},\qquad n\ge2$$.Тут \qquad означає “double quad”, де “quad” означає певний обсяг простору, який є звичайним для принтерів. Таким чином, \quad означає чотирикутник простору принтера в горизонтальному напрямку. Щоразу, коли вам потрібні інтервали, які відрізняються від звичайних угод, ви повинні вказати їх явно за допомогою таких команд, як \quad і \qquad.
Раніше квадроцикл був квадратним шматком порожнього типу, 1 ем завширшки та 1 ем заввишки - приблизно розмір великої літери М; але квадроцикл LaTeX не має висоти.
У тексті абзацу формули виглядають краще, якщо вони розділені словами, а не тільки комами. Але якщо тексту для вставки справді немає, вам слід принаймні залишити пробіл між формулами. Порівняйте
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, $n\ge2$.і
1The Fibonacci numbers satisfy $F_{n}=F_{n-1}+F_{n-2}$, \ $n\ge2$.які дають
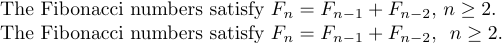
«\» тут забезпечує візуальне розділення, яке частково компенсує поганий стиль.
8.4. Інтервали у формулах
Ми вже бачили, що TeX виконує автоматичне розміщення інтервалів у математичних формулах, завдяки чому в більшості випадків вони виглядають правильно. Однак природно, що виникають винятки, оскільки кількість можливих формул величезна, а правила розміщення інтервалів у TeX досить прості. Отже, для таких випадків бажано мати дрібні одиниці інтервалу замість великих частин, які виникають із \ , \quad і \qquad.
Основні елементи простору, які TeX додає у формули, називаються тонкими пробілами, середніми пробілами та товстими пробілами. TeX автоматично вставляє їх у формули, але ви можете будь-коли додати власні інтервали за допомогою команд
Формули, які включають обчислення, виглядають найкраще, коли перед dx, dy або d вставлено додатковий тонкий пробіл; але TeX не робить це автоматично. Наступні приклади показують, як повідомити TeX про ці потреби:
Зауважте, що після «/» у передостанній формулі не було потрібно «,». Також немає потреби в \, в останньому прикладі, оскільки dt з’являється сам по собі в чисельнику дробу; це візуально відокремлює його від решти формули.
Фізичні одиниці, коли вони з’являються у формулі, мають бути встановлені латинським шрифтом і відділені від попереднього матеріалу тонким інтервалом:
Тонкі пробіли слід також вставляти після знаків оклику (операція факторіалу), якщо наступний символ є літерою, цифрою або відкриваючим роздільником:
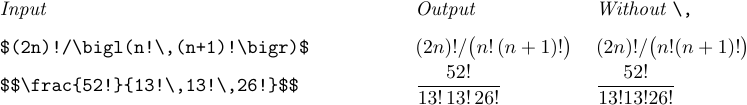
Крім цих випадків, ви час від часу зустрічатиметеся з формулами, у яких символи зібрані надто щільно або де з’являється забагато білого простору через певні невдалі комбінації форм. Зі смаком застосовані \, або \! відкривають або закривають речі, щоб читач не відволікався від математичного значення формули. Радикали та кратні інтеграли часто є кандидатами на таке тонке налаштування. Ось кілька прикладів ситуацій, на які варто звернути увагу:
Правила розміщення інтервалів у TeX іноді не вдаються, коли ‘|’ і ‘\|’ з’являються у формулі, оскільки ці символи розглядаються як звичайні символи, а не як роздільники. Розгляньте формули
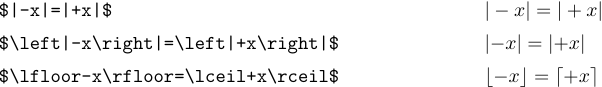
У першому випадку інтервал неправильний, оскільки TeX вважає, що знак плюс обчислює суму ‘|’ і ‘x’. Використання \left і \right у другому прикладі ставить TeX на правильний шлях. Третій приклад показує, що такі виправлення не потрібні для інших роздільників, тому що TeX знає, чи є вони відкриттям чи закриттям.
8.5. Еліпси
Три крапки можуть позначатися двома різними видами точок, одна вища за іншу. Найкращі традиції розрізняють ці дві можливості. Загалом правильно створювати такі формули, як
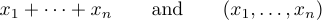
але неправильно створювати такі формули
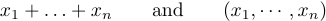
Ідея полягає в тому, щоб ввести \ldots, коли вам потрібні три нижні крапки, і \cdots, коли ви хочете три крапки по центру по вертикалі. Загалом, найкраще використовувати \cdots між + і - і знаками множення, а також між знаками = або знаками «менше або дорівнює», або знаками підмножини або іншими подібними відносинами. Крапки використовуються між комами, а також коли предмети розташовані поруч без жодних знаків між ними:
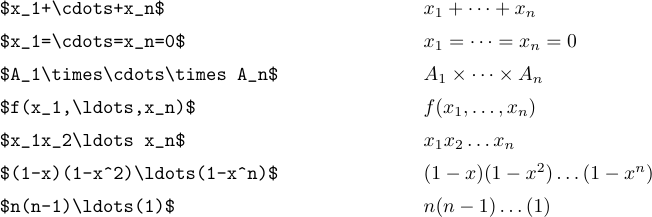Але є окремий випадок, коли \ldots і \cdots не створюють правильний інтервал. Це трапляється, коли вони з’являються в самому кінці формули або безпосередньо перед закриваючим роздільником. У таких ситуаціях необхідний додатковий тонкий простір. Наприклад, розглянемо такі речення:
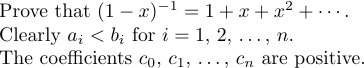
Перше речення створюється шляхом друкування
1Prove that $(1-x)^{-1}=1+x+x^2+\cdots\,$.Без \ крапка була б надто близькою до \cdots.
Друге речення було надруковано так:
1Clearly $a_i<b_i$ for $i=1$,~2, $\ldots\,$,~$n$.Зверніть увагу на використання зв’язків (~), які запобігають неправильним розривам рядків. Такі еліпси дуже поширені в деяких формах математичного запису, тому LaTeX надає макрос \dots як абревіатуру $\ldots\,$ для використання в тексті абзацу. Отже, третє речення можна надрукувати
1The coefficients $c_0$, $c_1$, \dots, ~$c_n$ are positive.8.6. Розрив лінії
Якщо у вас є формули в абзаці, TeX може розбити їх між рядками. Він розриває формулу лише після символу відношення або після символу двійкової операції, де відношення або двійкова операція знаходяться на зовнішньому рівні формули, тобто не укладені в {...}. Наприклад, якщо ви друкуєте
1$f(x,y) = x^2-y^2 = (x+y)(x-y)$в середині абзацу, існує ймовірність, що TeX зламається після будь-якого зі знаків = (бажано) або після - або + або - (в екстреній ситуації). Але розриву після коми в жодному разі не буде, оскільки коми, після яких бажано розбити розриви, не повинні стояти між $.
Якщо ви не хочете дозволяти порушення в цьому прикладі, окрім символів =, ви можете ввести
1$f(x,y) = {x^2-y^2} = {(x+y)(x-y)}$тому що ці додаткові дужки «заморожують» підформули, поміщаючи їх у непорушні коробки. Але немає потреби турбуватися про такі речі, якщо тільки TeX не порушує формулу, оскільки ймовірність цього досить низька.
Якщо ви все-таки хочете дозволити порушення на якомусь етапі на зовнішньому рівні формули, ви можете сказати \allowbreak. Наприклад, якщо формула
1$(x_1,\ldots,x_m,\allowbreak y_1,\ldots,y_n)$з’являється в тексті абзацу, TeX дозволить розбити його на дві частини
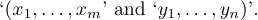
8.7. Брекети
Символи ‘{’ і ‘}’ використовуються в ряді різних нотацій, і LaTeX надає деякі команди, які допоможуть вам впоратися з формулами, що містять такі речі. Найпростіший випадок, коли дужки використовуються для позначення набору елементів. Наприклад, “{a, b, c}” означає набір із трьох елементів a, b і c:
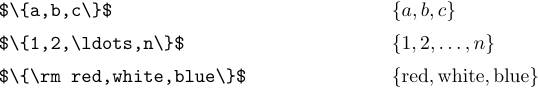
Набір також можна вказати за допомогою загального елемента, за яким слідує конкретна умова. Наприклад, набір усіх об’єктів x, які перевищують 5, можна записати так:
Це два варіанти для позначення одного набору. Перший вимагає використання \mid для отримання вертикальної смуги, а другий не вимагає нічого, крім двокрапки, яка розглядається як двійкова операція.
Коли роздільники стають більшими, їх слід називати \bigl, \bigm і \bigr:
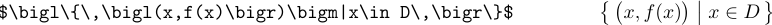
Формули з ще більшими роздільниками використовували б команди \Big або \bigg або навіть \Bigg.
Ви також можете знайти інше використання дужок у показаних формулах. Насправді це одна ліва дужка, яка вказує на вибір між кількома альтернативами:
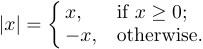
Цю конструкцію можна ввести за допомогою команди \case:
1$$|x|=\case{x,&if $x\ge0$;\cr
2 -x,&otherwise.\cr}$$Кожен із випадків складається з двох частин, розділених символом &, який відіграє особливу роль у побудові табличних структур. Ліворуч від & є математична формула, яка неявно укладена в $...$; праворуч від & — звичайний текст. Отже, -x у другому рядку буде набрано в математичному режимі, але otherwise буде набрано в горизонтальному режимі. Пробіли перед і після “&” ігноруються. Випадків може бути будь-яка, хоча зазвичай їх лише два. За кожним регістром має стояти \cr.
Горизонтальні дужки будуть встановлені над або під частинами показаної формули, якщо ви використовуєте команди \overbrace або \underbrace. Такі речі вважаються великими операторами, як-от \sum, тому ви можете встановити обмеження вище або нижче них, вказавши верхні або нижні індекси:
8.8. Матриці
Матриці є досить поширеними об’єктами в математичних формулах; це просто прямокутні масиви формул, розташованих у рядках і стовпцях. LaTeX надає команду \matrix для роботи з найпоширенішими типами матриць.
Наприклад, припустімо, що ви хочете вказати відображення
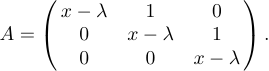
Усе, що ви робите, це друкувати
1$$A=\left(\matrix{x-\lambda&1&0\cr
2 0&x-\lambda&1\cr
3 0&0&x-\lambda\cr}\right).$$Це дуже схоже на конструкцію \cases, яку ми розглядали раніше; кожен рядок матриці слідує за \cr, а знаки & використовуються між окремими записами кожного рядка. Однак, на відміну від \cases, ви повинні розмістити власні розділювачі \left і \right навколо матриці. Причина полягає в тому, що різні роздільники можуть використовуватися в різних конструкціях матриці. З іншого боку, дужки використовуються частіше, ніж інші роздільники, тому ви можете ввести \pmatrix, якщо хочете, щоб LaTeX встановив дужки для вас:
1$$\pmatrix{x-\lambda&...&x-\lambda\cr}.$$Кожен запис матриці зазвичай центрується у своєму стовпці, і кожен стовпець розширюється настільки, наскільки це необхідно для розміщення записів, які він містить, а між стовпцями є чотирикутний простір. Якщо ви хочете, щоб щось виходило ліворуч/праворуч у своєму стовпчику, слідуйте/поставте перед ним \hfill.
Кожен запис матриці обробляється окремо від інших, і він набирається як математична формула у стилі тексту. Таким чином, наприклад, якщо ви скажете \rm в одному записі, це не вплине на інші. Сказати {\rm x&y} недійсно.
Матриці часто відображаються як загальні шаблони, які використовують еліпси для позначення пропущених рядків або стовпців. Ви можете набирати такі матриці, розміщуючи еліпси в їхніх власних рядках і/або стовпцях. Окрім \ldots, LaTeX надає \vdots (вертикальні точки) і \ddots (діагональні точки) для таких конструкцій. Розглянемо наступну матрицю
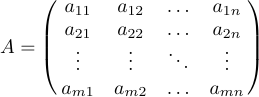
що визначено як:
1$$A=\pmatrix{a_{11}&a_{12}&\ldots&a_{1n}\cr
2 a_{21}&a_{22}&\ldots&a_{2n}\cr
3 \vdots&\vdots&\ddots&\vdots\cr
4 a_{m1}&a_{m2}&\ldots&a_{mn}\cr}$$Іноді матриця облямована зверху та зліва формулами, які дають мітки рядкам і стовпцям. Для цієї ситуації в LaTeX визначено спеціальний макрос під назвою \bordermatrix. Наприклад, дисплей
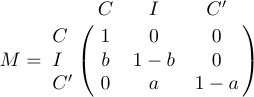
виходить під час введення
1$$M=\bordermatrix{&C&I&C'\cr
2 C&1&0&0\cr
3 I&b&1-b&0\cr
4 C'&0&a&1-a\cr}$$Перший рядок містить верхні мітки, які з’являються над великими лівими та правими дужками; перший стовпець містить ліві мітки, які набираються врівень зліва, безпосередньо перед самою матрицею. Елемент на перетині першого стовпця та першого рядка зазвичай порожній. І як \pmatrix, \bordermatrix вставляє власні дужки.
Вставляти матриці в текст абзацу зазвичай недоцільно. Причина в тому, що вони настільки великі, що краще відображаються. Але все ж іноді ви можете нехтувати цим. У цьому випадку ви можете використовувати \choose або \atop:
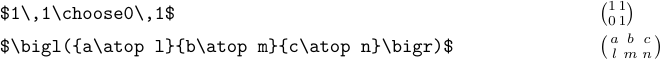
Макрос \matrix не створює таких малих масивів.