Matriz de transformación – ejemplos de código SVG
Scalable Vector Graphics (SVG) es un lenguaje XML para crear gráficos vectoriales bidimensionales y gráficos vectoriales/rasterizados mixtos. Y una matriz de transformación es una matriz que transforma un vector en otro vector en el proceso de multiplicación de matrices. Por lo tanto, es una herramienta conveniente para aplicar transformaciones SVG como translation, rotation, scaling y skewing. Las matrices de transformación se basan en álgebra lineal, que ofrece una forma matemáticamente elegante de expresar transformaciones complejas. Esta base matemática facilita que los desarrolladores y diseñadores con experiencia en matemáticas trabajen con transformaciones SVG.
¡Echemos un vistazo más de cerca a cómo funciona!
Matriz de transformación
La matriz de transformación es 3x3 y combina transformaciones de traslación, escala, rotación y sesgo. Esto es lo que representa cada elemento:
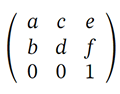
a – puede ser un factor de escala en la dirección x, generalmente indicado como sx o el valor del coseno cos(α) del ángulo a rotar
b – puede ser tan(α) factor de sesgo en la dirección y o el valor del seno sin(α) del ángulo a rotar
c – puede ser tan(α) factor de sesgo en la dirección x o el valor del seno -sin(α) del ángulo a rotar
d – puede ser un factor de escala en la dirección y que generalmente se denota como sy o el valor del coseno cos(α) del ángulo a rotar
e – la traslación a lo largo de la dirección x generalmente se indica como tx
f – la traslación a lo largo de la dirección y generalmente se denota como ty
La matriz de transformación le permite obtener nuevas coordenadas de los puntos del objeto (x nuevo, y nuevo) durante la transformación multiplicándola por los valores de las coordenadas anteriores (x prev, y prev):
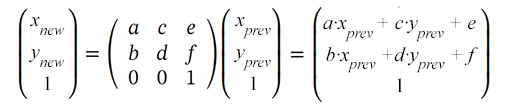
Los objetos SVG se pueden modificar utilizando la propiedad de matriz del atributo de transformación: transform=“matrix(a,b,c,d,e,f)”. Sólo se pueden especificar los primeros 6 valores. Por lo tanto, proporciona 6 valores a la función de transformación matricial para establecer la traslación, el escalado, la rotación y la inclinación.
Matriz de traducción – Translation Matrix
La translation es una transformación en SVG que mueve todos los puntos de un objeto a la misma distancia a lo largo de líneas paralelas. Esta transformación cambia el origen del sistema de coordenadas del elemento. La matriz de traducción se ve así:
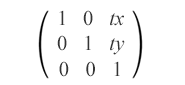
matrix(1,0,0,1,tx,ty)
La matriz de translation combina los valores tx y ty para mover un elemento horizontal y verticalmente. Desplaza el objeto tx a lo largo del eje x y ty a lo largo del eje y.
Mire el ejemplo con el rectángulo azul original que se traslada a lo largo del eje x (rojo), el eje y (naranja) y ambos (verde):
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <!-- no translation -->
4 <circle cx="15" cy="15" r="10" stroke="blue" />
5 <!-- horizontal translation by tx=30 -->
6 <circle cx="15" cy="15" r="10" stroke="red" transform="matrix(1 0 0 1 30 0)" />
7 <!-- vertical translation by by ty=25 -->
8 <circle cx="15" cy="15" r="10" stroke="orange" transform="matrix(1 0 0 1 0 25)" />
9 <!-- both horizontal and vertical translation by tx=30 and by ty=25 -->
10 <circle cx="15" cy="15" r="10" stroke="green" transform="matrix(1 0 0 1 30 25)" />
11 </g>
12</svg>La acción del atributo transform=“matrix(1,0,0,1,tx,ty)” significa el cambio de las coordenadas del objeto según la fórmula:
x(new) = a·x(prev) + b·y(prev) +e = x(prev) + tx
y(new) = b·x(prev) + d·y(prev) +f = y(prev) + ty
En el ejemplo de código, el elemento <g> se utiliza para agrupar círculos. El atributo fill se aplica dentro de <g> a todas las formas una vez. Aquí está la imagen resultante:
Matriz de escala – Scaling Matrix
El escalado es una transformación SVG que amplía o reduce un objeto utilizando un factor de escala. Se utiliza una matriz de escala para escalar objetos de manera uniforme o no uniforme a lo largo de los ejes de coordenadas. sx y sy son los factores de escala para los ejes x y y. Si sx y sy son mayores que 1, el objeto se ampliará; si están entre 0 y 1, el objeto se reducirá. Si los factores de escala se establecen en valores diferentes, la escala del objeto será desigual, lo que dará como resultado un efecto de estiramiento o encogimiento. La matriz de escala se ve así:
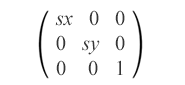
matrix(sx,0,0,sy,0,0)
Mire el ejemplo con el rectángulo azul original que escala uniformemente y no uniformemente, en relación con el origen (0, 0): imágenes a y b, y escala uniformemente en relación con el punto (10, 10), imagen c:
1<svg viewBox="0 0 400 300" xmlns="http://www.w3.org/2000/svg">
2 <!-- uniform scale is shown in fig.a -->
3 <g fill="none">
4 <rect x="10" y="10" width="20" height="20" stroke="blue" />
5 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, 0, 0)" />
6 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, 0, 0)" />
7 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 0, 0)" />
8 </g>
9 <!-- non-uniform scale is shown in fig.b -->
10 <g transform="translate(70)">
11 <rect x="10" y="10" width="20" height="20" fill="blue" />
12 <rect x="10" y="10" width="20" height="20" fill="red" transform="matrix(1.5, 0, 0, 2, 0, 0)" />
13 <rect x="10" y="10" width="20" height="20" fill="orange" transform="matrix(3, 0, 0, 2.5, 0, 0)" />
14 <rect x="10" y="10" width="20" height="20" fill="green" transform="matrix(0.7, 0, 0, 0.5, 0, 0)" />
15 </g>
16 <!-- uniform scale relative to point (10, 10) is shown in fig.c -->
17 <g fill="none" transform="translate(170)">
18 <rect x="10" y="10" width="20" height="20" stroke="blue" />
19 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, -5, -5)" />
20 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, -10, -10)" />
21 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 3, 3)" />
22 </g>
23</svg>Aquí está la imagen resultante:
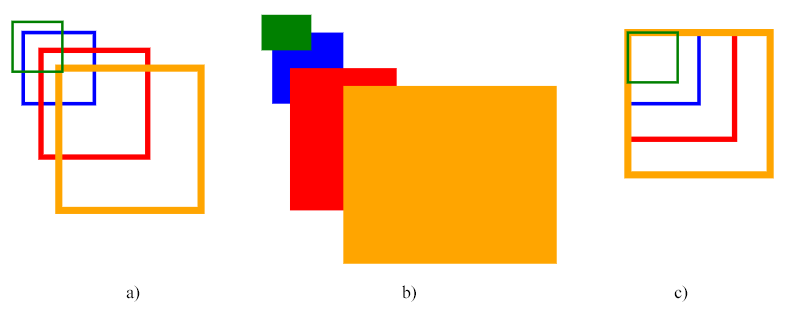
El código anterior utiliza la matriz de escala. El primer grupo de rectángulos en la figura muestra un ejemplo de escala uniforme (fig. a), el segundo grupo ilustra la escala no uniforme (fig. b) y el tercer grupo de rectángulos muestra la escala uniforme relativa al punto (10 , 10): la esquina superior izquierda del rectángulo azul (fuente).
Nota: La escala se realiza en relación con el origen (0, 0) del sistema de coordenadas. Si el punto (cx, cy) del objeto SVG (se dibuja en relación con) no está en el origen, aplicar una transformación de escala cambiará la posición del objeto, lo que puede dar la impresión de translation. Vemos el efecto de la traslación de los rectángulos en las figuras a y b.
Para escalar alrededor de un punto de pivote específico (сx, сy), debe aplicar un movimiento adicional a la forma escalada para moverla al punto de pivote (fig. c). Matriz de transformación completa que combina traducción y escalado:
matrix(sx,0,0,sy,cx·(1-sx),cy·(1-sy))
Esta matriz escalará correctamente el objeto alrededor del punto de pivote (cx, cy) sin ninguna traducción. Los coeficientes cx·(1-sx) y cy·(1-sy) manejan la traducción necesaria para garantizar que el objeto permanezca en su posición original después del escalado. Calculemos estos valores para el rectángulo rojo (fig. c). El punto de pivote (cx, cy) en este ejemplo es (10, 10): la esquina superior izquierda del rectángulo azul (inicial):
cx·(1-sx)=10·(1-1.5)=10·(-0.5)=-5
cy·(1-sy)=10·(1-1.5)=10·(-0.5)=-5
Puede cambiar el tamaño de SVG en C# usando Aspose.SVG for .NET API. El artículo
Escalado SVG: ejemplos de C# cubre ejemplos de C# para el escalado SVG. Encontrará casos de uso de la función scale() en el atributo transform así como una matriz de transformación – matrix(a,b,c,d,e,f).
Matriz de rotación – Rotation Matrix
Si te gusta practicar el cálculo de senos y cosenos, ¡estás aquí! La matriz de rotación se ve así:
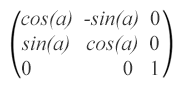
matrix(cos(α),sin(α),-sin(α),cos(α),0,0), donde α es el ángulo alrededor del punto con coordenadas (0, 0) del sistema de coordenadas inicial.
Mire el ejemplo con un rectángulo azul inicial, que está girado 90° (verde), 180° (gris), 270° (verde azulado), -45° (rojo) y 135° (naranja):
1<svg viewBox="-50 -50 200 200" xmlns="http://www.w3.org/2000/svg">
2 <!-- rotation around point with coordinates (0, 0) is shown in fig.a -->
3 <g>
4 <rect x="0" y="0" width="20" height="20" fill="blue" />
5 <rect x="0" y="0" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
6 <rect x="0" y="0" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
7 <rect x="0" y="0" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
8 <rect x="0" y="0" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
9 <rect x="0" y="0" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
10 <!-- rotation around point with coordinates (0, 0) is shown in fig.b -->
11 </g>
12 <g transform="translate(70)">
13 <rect x="5" y="5" width="20" height="20" fill="blue" />
14 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
15 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
16 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
17 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
18 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
19 </g>
20 <!-- rotation around point with coordinates (5, 5) is shown in fig.c -->
21 <g transform="translate(140)">
22 <rect x="5" y="5" width="20" height="20" fill="blue" />
23 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 10, 0)" />
24 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 10, 10)" />
25 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 10)" />
26 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, -2, 5)" />
27 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 12, 5)" />
28 </g>
29</svg>Nota: Si usamos un valor de ángulo positivo, entonces la rotación será en el sentido de las agujas del reloj y, a la inversa, un valor de ángulo negativo nos dará un giro en el sentido contrario a las agujas del reloj.
El resultado de la rotación SVG se puede ver en la figura:
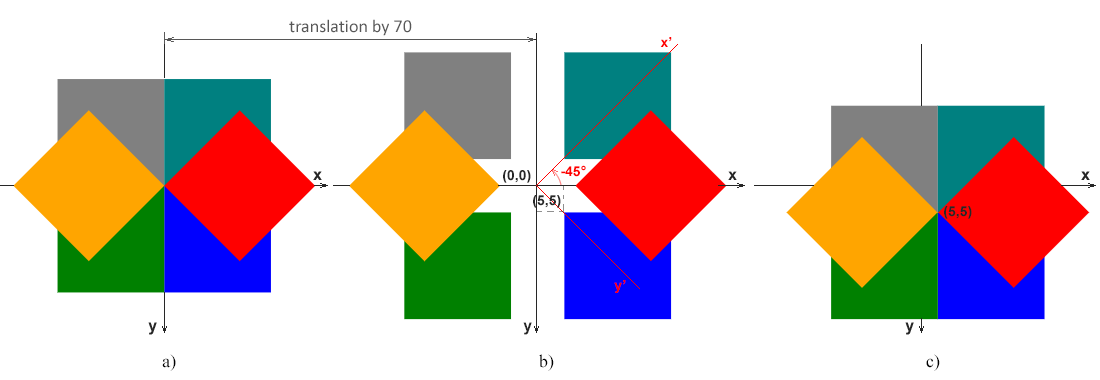En fig. a muestra el caso en el que la esquina superior izquierda del rectángulo azul (inicial) (0, 0) coincide con el punto de origen del sistema de coordenadas (0, 0).
En fig. b ilustra el caso en el que la esquina superior izquierda del rectángulo azul (inicial) (5, 5) no coincide con el punto de origen (0, 0). Esta figura muestra los ejes x-y del sistema de coordenadas original, que son válidos para todas las figuras a, b y c. Además, los ejes x’-y’ del sistema de coordenadas del rectángulo rojo, que se gira 45 grados en sentido contrario a las agujas del reloj α=-45°, se muestran en rojo. Esto muestra claramente que la rotación del rectángulo se reduce a la rotación del sistema de coordenadas.
En fig. c muestra el caso en el que la esquina superior izquierda del rectángulo azul (inicial) (5, 5) no coincide con el punto inicial del sistema de coordenadas (0, 0), pero la rotación se produce alrededor del punto (5, 5).
Nota: La siguiente matriz rotará el objeto alrededor del punto de pivote (cx, cy):
matrix(cos(α), sin(α), -sin(α), cos(α), cx·(1-cos(α))+cy·sin(α), cy·(1-cos(α))-cx·sin(α))
Los coeficientes cx·(1-cos(α))+cy·sin(α) y cy·(1-cos(α))-cx·sin(α) manejan la traslación necesaria para asegurar que el objeto permanezca en su posición original después de la rotación. Calculemos estos valores para el rectángulo rojo (fig. c). El punto de pivote (cx, cy) en este ejemplo es (5, 5): la esquina superior izquierda del rectángulo azul (inicial) y el ángulo del rectángulo rojo es -45°:
cos(-45°)=0,7071, sen(-45°)=-0,7071
cx·(1-cos(α))+cy·sin(α)=5·(1-0.7071)+5·(-0.7071)=-2
cy·(1-cos(α))-cx·sin(α)=5·(1-0.7071)-5·(-0.7071)=5
Puede rotar SVG en C# usando Aspose.SVG for .NET API. El artículo
Rotar SVG – Ejemplos de C# cubre ejemplos de C# para la rotación de SVG. Considera casos de uso de la función rotate() en el atributo transform y la matriz de transformación – matrix(a,b,c,d,e,f).
Matriz sesgada – Skewing Matrix
La inclinación es una transformación que gira uno de los ejes del sistema de coordenadas del elemento en un cierto ángulo α en el sentido de las agujas del reloj o en el sentido contrario a las agujas del reloj. Los elementos SVG se pueden sesgar mediante el uso de la matriz de sesgo que se ve así:
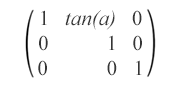
matrix(1,0,tan(α),1,0,0): esta matriz sesgada especifica una transformación sesgada a lo largo del eje x en α grados.
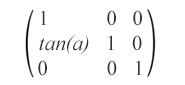
matrix(1,tan(α),0,1,0,0): esta matriz sesgada especifica una transformación sesgada a lo largo del eje y en α grados.
A continuación se muestra un ejemplo del círculo con transformaciones sesgadas:
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <circle cx="20" cy="20" r="10" stroke="blue" />
4 <!-- skew transformation along the x-axis by α=45° -->
5 <circle cx="20" cy="20" r="10" stroke="red" transform="matrix(1,0,1,1,0,0)" />
6 </g>
7 <g fill="none" transform="translate(70)">
8 <circle cx="20" cy="20" r="10" stroke="blue" />
9 <!-- skew transformation along the y-axis by α=45° -->
10 <circle cx="20" cy="20" r="10" stroke="orange" transform="matrix(1,1,0,1,0,0)" />
11 </g>
12</svg>El ejemplo renderizado se ve así:
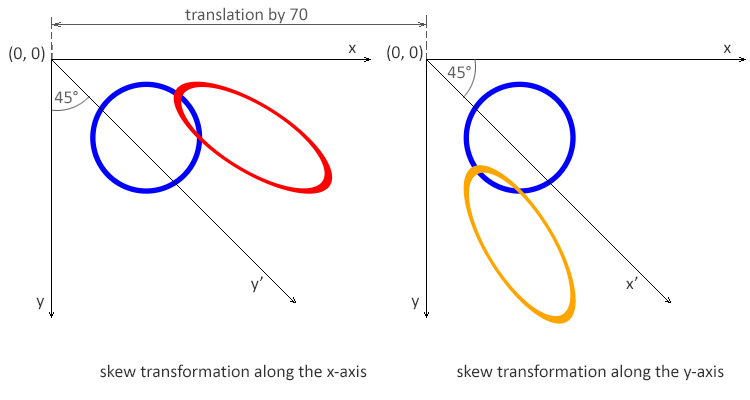
Nota: El valor del ángulo α representa una transformación SVG sesgada en grados a lo largo del eje apropiado. Al usar la transformación sesgada a lo largo del eje x, solo cambia la coordenada x de los puntos de la forma, pero la coordenada y permanece sin cambios. La transformación sesgada a lo largo del eje x hace que las líneas verticales parezcan haber sido giradas en un ángulo determinado. La coordenada x de cada punto cambia en un valor proporcional al ángulo especificado y la distancia al origen.
Conclusión
La matriz de transformación SVG es una poderosa herramienta para manipular y animar objetos en SVG. Proporciona una forma versátil de aplicar traslación, rotación, escalado e inclinación a formas y elementos, lo que le permite crear gráficos visualmente dinámicos e interactivos. La matriz permite transformaciones individuales y combinadas, ofreciendo la flexibilidad para lograr efectos visuales complejos e intrincados. Solo hemos cubierto transformaciones individuales en este artículo, pero pronto intentaremos ampliar nuestra guía de dibujo SVG con nuevos artículos con ejemplos más complejos.
Para obtener más información y obtener ejemplos de código SVG para rotar, escalar, mover y sesgar gráficos SVG usando el atributo de transformación SVG, consulte el artículo Transformación SVG.
Lea el artículo Transformaciones SVG – Ejemplos de C# para obtener ejemplos de código C# para rotar, escalar, traducir y sesgar gráficos SVG usando Aspose.SVG para la biblioteca .NET.
Aspose.SVG ofrece Aplicaciones web gratuitas SVG para convertir archivos SVG o de imágenes, fusionar archivos SVG, vectorizar imágenes, generar sprites SVG, codificar datos SVG a base64 y más. Estas aplicaciones en línea funcionan en cualquier sistema operativo con un navegador web y no requieren instalación de software adicional. ¡Es una manera rápida y fácil de resolver de manera eficiente y efectiva sus tareas relacionadas con SVG!