7. Delimiters | LaTeX manual | Aspose.TeX

Whatever large a math formula may get, TeX knows a way of making some symbols large enough to have proper appearance. For example, the result of typing

$$\sqrt{1+\sqrt{1+\sqrt{1+
            \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+x}}}}}}}$$

shows a variety of available radical, or square root, signs:

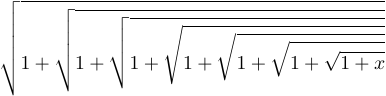
The three largest signs here are the same, except for a vertical segment that gets repeated as many times as necessary to reach the required size. At the same time, the smaller signs are distinct characters taken from TeX’s math fonts.

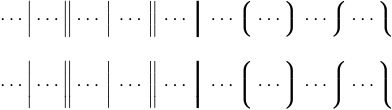
Something similar happens with parentheses and other so-called “delimiter” symbols. Such symbols are important in mathematics, because they give visual clues to the underlying structure of complex expressions. In other words, they limit boundaries of individual subformulas. Here is the list of the 22 basic delimiters provided by LaTeX:

To get a slightly larger version of any of these symbols, just type \bigl or \bigr for opening or closing delimiters, respectively. This makes formulas with nested delimiters easier to read:

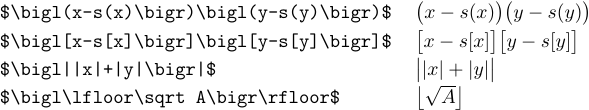
The \big delimiters are just enough bigger than ordinary ones so that the difference can be noticed, and yet small enough to be used in the text of a paragraph:

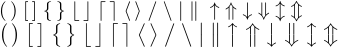
You can get one more step larger symbols suitable for displays, if you type \Bigl and \Bigr instead of \bigl and \bigr:

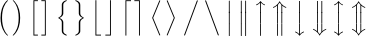
These are 50% taller than the versions in the previous step. Displayed formulas often use even taller delimiters (twice the size of \big). You can get them by typing \biggl and \biggr:

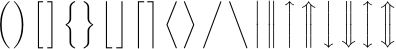
Finally, you can type \Biggl and \Biggr versions, 2.5 times as tall as the \bigl and \bigr delimiters:

LaTeX also provides \bigm, \Bigm, \biggm, and \Biggm commands to produce delimiters that can be used in the middle of formulas. Such a delimiter acts like a relation, so TeX puts a bit of space on either side of it:

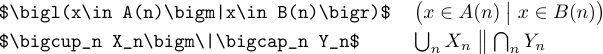
It’s also possible to say just \big, \Big, \bigg, or \Bigg to produce a delimiter that behaves like an ordinary variable. These commands would primarily be used with slashes and backslashes:

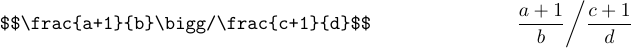
TeX implements an algorithm that figures out how tall a pair of delimiters needs to be, in order to enclose a given subformula. You can use it, instead of deciding whether a delimiter should be \big or \bigg or whatever. Just say

\left<delim1><subformula>\right<delim2>

and TeX will typeset a subformula, putting the specified delimiters at the left and at the right. The size of the delimiters will be just big enough to cover the subformula:

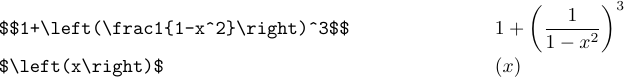
When you use \left and \right they must be paired up, just as braces do groups. You can’t have \left in one subformula and \right in another. Also, you can’t type things like \left(...{...\right...} or \left(...\begingroup...\right)...\endgroup. This is because TeX needs to typeset the subformula that appears between \left and \right before it can decide how big to make the delimiters. When you are not using \left and \right, you don’t have to match the parentheses and brackets. Thus you are allowed to type something like $[0,1)$ or $)($ or even $)$. And even when you do use \left and \right, you don’t have to match the particular symbols, so that \left) or \right( will not cause an error.

But why bother learning about \bigl and \bigr and others of their kind, when TeX can automatically calculate sizes for \left and \right? There are at least three cases in which you would want to decide by yourself on selecting the proper delimiter size:

(1) Just compare the following two formulas:

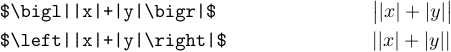
Indeed, using \left and \right wasn’t a wise choice, as they couldn’t figure out the delimiter size appropriate for the best readability.

(2) On the other hand, sometimes \left and \right choose a larger delimiter than you want. This happens mostly when they enclose a large operator in a display:

The TeX’s algorithm causes \left and \right to enclose the \sum together with its limits, but in special cases like this it looks better to let the limits hang out a bit. So \bigg delimiters are better here.

(3) When you need to typeset a huge displayed formula, you have to break it into two or more lines. And you want to make sure that its opening and closing delimiters have the same size; but you can’t use \left on the first line and \right on the last, since \left and \right must occur in pairs. The only solution is to use \Biggl (for example) on the first line and \Biggr on the last.

Although \left and \right usually can make arbitrarily large delimiters, the slashes and angle brackets do have a maximum size. If you ask for really big versions of those symbols you will get the largest ones available.

You can also use a trick that produces a so-called null (blank) delimiter. You would need such a delimiter when you need to typeset a formula that visually contains only one large delimiter. For example,

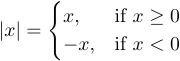
has ‘{’ but no ‘}’. It can be produced by a construction of the form

$$|x|=\left\{ ... \right.$$ 

where \right. generates the right null delimiter.

LaTeX also provides a few more delimiters, which are not listed in the basic set of 22 because they are sort of special. The commands \arrowvert, \Arrowvert, and \bracevert produce delimiters made from the repeatable parts of the vertical arrows, double vertical arrows, and large braces, respectively, without arrowheads or the curly parts of the braces. They produce results similar to \vert and \Vert, but they are surrounded by more white space and they have a different weight. There are also \lgroup and \rgroup, which are constructed from braces without the middle parts; and \lmoustache and \rmoustache, which produce the top and bottom halves of large braces. Here are displays with the \Big and \bigg versions of \vert, \Vert, and these seven special delimiters:

You can find that \lgroup and \rgroup are rather like bold parentheses, with sharper bends at the corners; this makes them attractive for certain large displays. Note that you can’t use them exactly like parentheses, because they are available only in sizes \Big and more.