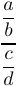5. Fractions, binomial coefficients and math styles

Another common thing you may find in math formulas is fractions and other constructions where something like a numerator is placed on top of something like a denominator. An example of the latter is binomial coefficients.

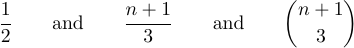
You can get these three formulas as displayed equations by typing $$1\over2$$ and $$n+1\over3$$ and $$\n+1\choose3$$.

The command \over applies to everything in the formula unless you enclose it in a specific subformula with braces, in which case \over applies to everything in that subformula.

You cannot use \over twice in the same subformula, i.e., type a\over b\over 2. Instead, you should explicitly specify what goes over what:

It seems that both formulas don’t look very nice. In such cases, it’s usually best to convert fractions to a “slashed form”. For example, the last two formulas should be typed as follows:

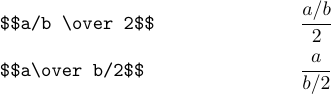
Here are more complex examples:

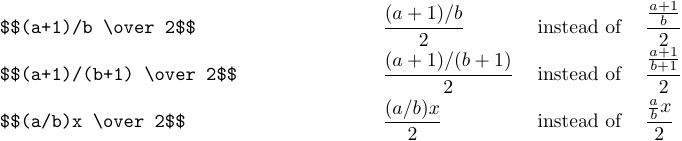
Looking at the examples above, you may have noticed that letters and other symbols sometimes get smaller when they appear in fractions, just as they get smaller when they are in subscripts or superscripts. Let’s now talk about the way TeX chooses the sizes of symbols. TeX has eight styles in which it can treat formulas:

• display style (for formulas displayed on lines by themselves)
• text style (for formulas embedded in text)
• script style (for subformulas used as superscripts or subscripts)
• scriptscript style (for second-order superscripts or subscripts) and four “cramped” styles that are almost the same except that subscripts and superscripts aren’t raised so much. We will refer to the eight styles as D, D’, T, T’, S, S’, SS, SS’, where D is display style, D’ is cramped display style, T is text style, etc. TeX also uses three sizes to type math formulas: text size, script size, and scriptscript size.

To typeset a formula in running text, you enclose it in $...$; this produces the formula in style T. Or you can enclose it in $$...$$ to get a displayed formula; this displays the formula in style D. The subformulas of a formula may be in different styles. Once you know the style, you can determine the size of type that TeX will use:

There is no “SSS” style since such tiny symbols would be even less readable than the scriptscript ones.

For example, if x^{a_b} is to be typeset in style D, the a_b will be set in style S, and b in style SS; the result is

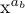
We haven’t seen any difference between styles D and T yet. There is actually a slight difference in the positioning of exponents, although script size is used in each case. But there is a big distinction between styles D and T in case of fractions:

So, if you type $1\over2$ (in a text) you get style S over style S’. But if you type $$1\over2$$ you get style T over style T’ in a displayed formula.

Finally, \underline does not change the style. Math accents, and the commands \sqrt and \overline change uncramped styles to their cramped counterparts retaining cramped styles.

It may happen that you don’t like the style that TeX selects according to its own rules. You are free to specify the desired style by typing \displaystyle or \textstyle or \scriptstyle or \scriptscriptstyle; the selected style will apply until the end of the formula or subformula, or until you select another style. For example, $$n+\scriptstyle n+\scriptscriptstyle n.$$ yields the following display:

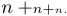
It shows that the plus sign gets smaller too as the style changes, and that TeX puts no space around + in script styles.

Let’s take a look at another example - a continued fraction.

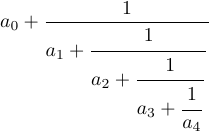
You can get it by typing

$$a_0+{1\over\displaystyle a_1+
        {\strut 1\over\displaystyle a_2+
          {\strut 1\over\displaystyle a_3+
            {\strut 1\over a_4}}}}$$

Without \strut and \displaystyle in this formula, the result would be different:

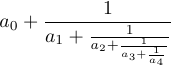
LaTeX defines the macro \frac that allows you to specify fractions using another syntax: \frac{a}{b} is equivalent to a\over b, and \frac12 is equivalent to 1\over2.

There is another operation \atop in TeX, which is like \over except that it doesn’t draw the fraction line:

The LaTeX format also defines \choose, which is like \atop but encloses the result in parentheses:

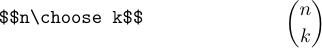
It is called \choose because it’s a common notation for the binomial coefficient that tells how many ways there are to choose k things out of n things.

The commands \over, \atop, and \choose cannot be mixed with each other. For example, $$n\choose k\over 2$$ is illegal. You must use grouping to get either $${n\choose k}\over2$$ or $$n\choose{k\over2}$$.

TeX has the \above command which is a generalized version of \over and \atop. In this command you specify the exact thickness of the line rule by typing \above<dimen>. For example,

$$\displaystyle{\frac{a}{b}\above1pt\displaystyle{\frac{c}{d}}$$

will produce a compound fraction with a 1pt thick rule between the fractions in the numerator and denominator: