Matrice de transformation – Exemples de code SVG
Scalable Vector Graphics (SVG) est un langage XML permettant de créer des graphiques vectoriels bidimensionnels et mixtes vectoriels/raster. Et une matrice de transformation est une matrice qui transforme un vecteur en un autre vecteur lors du processus de multiplication matricielle. C’est donc un outil pratique pour appliquer des transformations SVG telles que la traduction, la rotation, la mise à l’échelle et l’inclinaison. Les matrices de transformation sont basées sur l’algèbre linéaire, qui offre une manière mathématiquement élégante d’exprimer des transformations complexes. Cette base mathématique permet aux développeurs et aux concepteurs ayant une formation en mathématiques de travailler plus facilement avec les transformations SVG.
Regardons de plus près comment cela fonctionne!
Matrice de transformation
La matrice de transformation est 3x3, combinant les transformations de translation, d’échelle, de rotation et d’inclinaison. Voici ce que représente chaque élément :
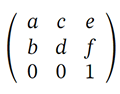
a – il peut s’agir d’un facteur d’échelle dans la direction x, généralement noté sx ou la valeur du cosinus cos(α) de l’angle de rotation
b – il peut s’agir du facteur d’inclinaison tan(α) dans la direction y ou de la valeur sinusoïdale sin(α) de l’angle à tourner
c – il peut s’agir du facteur d’inclinaison tan(α) dans la direction x ou de la valeur sinusoïdale -sin(α) de l’angle à tourner
d – il peut s’agir d’un facteur d’échelle dans la direction y, généralement noté sy ou la valeur du cosinus cos(α) de l’angle à faire pivoter
e – la translation dans la direction x est généralement notée tx
f – la translation dans la direction y est généralement notée ty
La matrice de transformation permet d’obtenir de nouvelles coordonnées des points de l’objet (x new, y new) lors de la transformation en la multipliant par les valeurs des coordonnées précédentes (x prev, y prev):
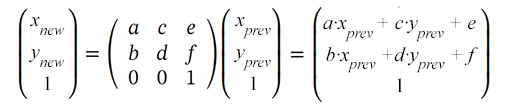
Les objets SVG peuvent être modifiés à l’aide de la propriété matrice de l’attribut transform: transform=“matrix(a,b,c,d,e,f)”. Seules les 6 premières valeurs peuvent être spécifiées. Vous fournissez donc 6 valeurs à la fonction de transformation matricielle pour définir la translation, la mise à l’échelle, la rotation et l’inclinaison.
Matrice de traduction – Translation Matrix
La translation est une transformation en SVG qui déplace tous les points d’un objet à la même distance le long de lignes parallèles. Cette transformation déplace l’origine du système de coordonnées de l’élément. La matrice de traduction ressemble à ceci:
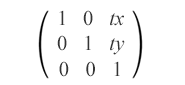
matrix(1,0,0,1,tx,ty)
La matrice de translation combine les valeurs tx et ty pour déplacer un élément horizontalement et verticalement. Il décale l’objet de tx le long de l’axe des x et de ty le long de l’axe des y.
Regardez l’exemple avec le rectangle bleu d’origine qui se traduit le long de l’axe des x (rouge), de l’axe des y (orange) et des deux (vert):
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <!-- no translation -->
4 <circle cx="15" cy="15" r="10" stroke="blue" />
5 <!-- horizontal translation by tx=30 -->
6 <circle cx="15" cy="15" r="10" stroke="red" transform="matrix(1 0 0 1 30 0)" />
7 <!-- vertical translation by by ty=25 -->
8 <circle cx="15" cy="15" r="10" stroke="orange" transform="matrix(1 0 0 1 0 25)" />
9 <!-- both horizontal and vertical translation by tx=30 and by ty=25 -->
10 <circle cx="15" cy="15" r="10" stroke="green" transform="matrix(1 0 0 1 30 25)" />
11 </g>
12</svg>L’action de l’attribut transform=“matrix(1,0,0,1,tx,ty)” signifie le changement des coordonnées de l’objet selon la formule:
x(nouveau) = a·x(prev) + b·y(prev) +e = x(prev) + tx
y(nouveau) = b·x(préc) + d·y(préc) +f = y(préc) + ty
Dans l’exemple de code, l’élément <g> est utilisé pour regrouper les cercles. L’attribut fill s’applique une fois à l’intérieur de <g> à toutes les formes. Voici l’image résultante:
Matrice de mise à l’échelle – Scaling Matrix
La mise à l’échelle est une transformation SVG qui agrandit ou réduit un objet à l’aide d’un facteur de mise à l’échelle. Une matrice de mise à l’échelle est utilisée pour mettre à l’échelle les objets de manière uniforme ou non uniforme le long des axes de coordonnées. sx et sy sont les facteurs d’échelle pour les axes x et y. Si sx et sy sont supérieurs à 1, l’objet sera agrandi ; s’ils sont compris entre 0 et 1, l’objet sera réduit. Si les facteurs d’échelle sont définis sur des valeurs différentes, l’échelle de l’objet sera inégale, ce qui entraînera un effet d’étirement ou de rétrécissement.
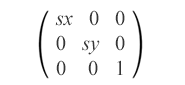
matrix(sx,0,0,sy,0,0)
Regardez l’exemple avec le rectangle bleu d’origine qui évolue de manière uniforme et non uniforme, par rapport à l’origine (0, 0) – images a et b, et qui évolue uniformément par rapport au point (10, 10) – image c:
1<svg viewBox="0 0 400 300" xmlns="http://www.w3.org/2000/svg">
2 <!-- uniform scale is shown in fig.a -->
3 <g fill="none">
4 <rect x="10" y="10" width="20" height="20" stroke="blue" />
5 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, 0, 0)" />
6 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, 0, 0)" />
7 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 0, 0)" />
8 </g>
9 <!-- non-uniform scale is shown in fig.b -->
10 <g transform="translate(70)">
11 <rect x="10" y="10" width="20" height="20" fill="blue" />
12 <rect x="10" y="10" width="20" height="20" fill="red" transform="matrix(1.5, 0, 0, 2, 0, 0)" />
13 <rect x="10" y="10" width="20" height="20" fill="orange" transform="matrix(3, 0, 0, 2.5, 0, 0)" />
14 <rect x="10" y="10" width="20" height="20" fill="green" transform="matrix(0.7, 0, 0, 0.5, 0, 0)" />
15 </g>
16 <!-- uniform scale relative to point (10, 10) is shown in fig.c -->
17 <g fill="none" transform="translate(170)">
18 <rect x="10" y="10" width="20" height="20" stroke="blue" />
19 <rect x="10" y="10" width="20" height="20" stroke="red" transform="matrix(1.5, 0, 0, 1.5, -5, -5)" />
20 <rect x="10" y="10" width="20" height="20" stroke="orange" transform="matrix(2, 0, 0, 2, -10, -10)" />
21 <rect x="10" y="10" width="20" height="20" stroke="green" transform="matrix(0.7, 0, 0, 0.7, 3, 3)" />
22 </g>
23</svg>Voici l’image résultante:
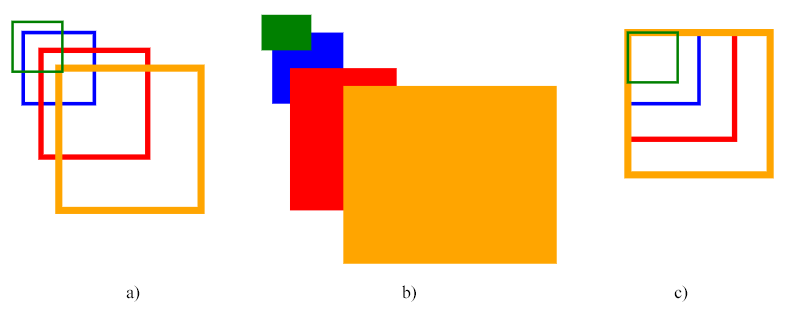
Le code ci-dessus utilise la matrice d’échelle. Le premier groupe de rectangles sur la figure affiche un exemple d’échelle uniforme (fig. a), le deuxième groupe illustre l’échelle non uniforme (fig. b) et le troisième groupe de rectangles montre l’échelle uniforme par rapport au point (10 , 10) – le coin supérieur gauche du rectangle bleu (source).
Remarque: La mise à l’échelle est effectuée par rapport à l’origine (0, 0) du système de coordonnées. Si le point (cx, cy) de l’objet SVG (il est dessiné par rapport à) n’est pas à l’origine, l’application d’une transformation de mise à l’échelle déplacera la position de l’objet, ce qui peut donner l’impression d’une translation. On voit l’effet de la translation des rectangles sur les figures a et b.
Afin de redimensionner autour d’un point pivot spécifique (сx, сy), vous devez appliquer un mouvement supplémentaire à la forme mise à l’échelle pour la déplacer vers le point pivot (fig. c). Matrice de transformation complète combinant traduction et mise à l’échelle:
matrix(sx,0,0,sy,cx·(1-sx),cy·(1-sy))
Cette matrice mettra correctement à l’échelle l’objet autour du point pivot (cx, cy) sans aucune translation. Les coefficients cx·(1-sx) et cy·(1-sy) gèrent la translation nécessaire pour garantir que l’objet reste à sa position d’origine après la mise à l’échelle. Calculons ces valeurs pour le rectangle rouge (fig. c). Le point pivot (cx, cy) dans cet exemple est (10, 10) – le coin supérieur gauche du rectangle bleu (initial) :
cx·(1-sx)=10·(1-1.5)=10·(-0.5)=-5
cy·(1-sy)=10·(1-1.5)=10·(-0.5)=-5
Vous pouvez redimensionner SVG en C# à l’aide de l’API Aspose.SVG pour .NET. L’article
Mise à l’échelle SVG – Exemples C# couvre des exemples C# pour la mise à l’échelle SVG. Vous pouvez trouver des cas d’utilisation de la fonction scale() dans l’attribut transform , ainsi qu’une matrice de transformation – matrix(a,b,c,d,e,f).
Matrice de rotation – Rotation Matrix
Si vous aimez vous entraîner à calculer les sinus et les cosinus, vous êtes ici! La matrice de rotation ressemble à ceci:
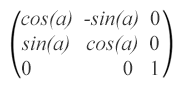
matrix(cos(α),sin(α),-sin(α),cos(α),0,0), où α est l’angle autour du point de coordonnées (0, 0) du système de coordonnées initial.
Regardez l’exemple avec le rectangle bleu initial, qui tourne à 90° (vert), 180° (gris), 270° (sarcelle), -45° (rouge) et 135° (orange):
1<svg viewBox="-50 -50 200 200" xmlns="http://www.w3.org/2000/svg">
2 <!-- rotation around point with coordinates (0, 0) is shown in fig.a -->
3 <g>
4 <rect x="0" y="0" width="20" height="20" fill="blue" />
5 <rect x="0" y="0" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
6 <rect x="0" y="0" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
7 <rect x="0" y="0" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
8 <rect x="0" y="0" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
9 <rect x="0" y="0" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
10 <!-- rotation around point with coordinates (0, 0) is shown in fig.b -->
11 </g>
12 <g transform="translate(70)">
13 <rect x="5" y="5" width="20" height="20" fill="blue" />
14 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 0, 0)" />
15 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 0, 0)" />
16 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 0)" />
17 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, 0, 0)" />
18 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 0, 0)" />
19 </g>
20 <!-- rotation around point with coordinates (5, 5) is shown in fig.c -->
21 <g transform="translate(140)">
22 <rect x="5" y="5" width="20" height="20" fill="blue" />
23 <rect x="5" y="5" width="20" height="20" fill="green" transform="matrix(0, 1, -1, 0, 10, 0)" />
24 <rect x="5" y="5" width="20" height="20" fill="grey" transform="matrix(-1, 0, 0, -1, 10, 10)" />
25 <rect x="5" y="5" width="20" height="20" fill="teal" transform="matrix(0, -1, 1, 0, 0, 10)" />
26 <rect x="5" y="5" width="20" height="20" fill="red" transform="matrix(0.7071, -0.7071, 0.7071, 0.7071, -2, 5)" />
27 <rect x="5" y="5" width="20" height="20" fill="orange" transform="matrix(-0.7071, 0.7071, -0.7071, -0.7071, 12, 5)" />
28 </g>
29</svg>Remarque: Si nous utilisons une valeur d’angle positive, alors la rotation se fera dans le sens des aiguilles d’une montre, et inversement, une valeur d’angle négative nous donnera une rotation dans le sens inverse des aiguilles d’une montre.
Le résultat de la rotation SVG est visible sur la figure:
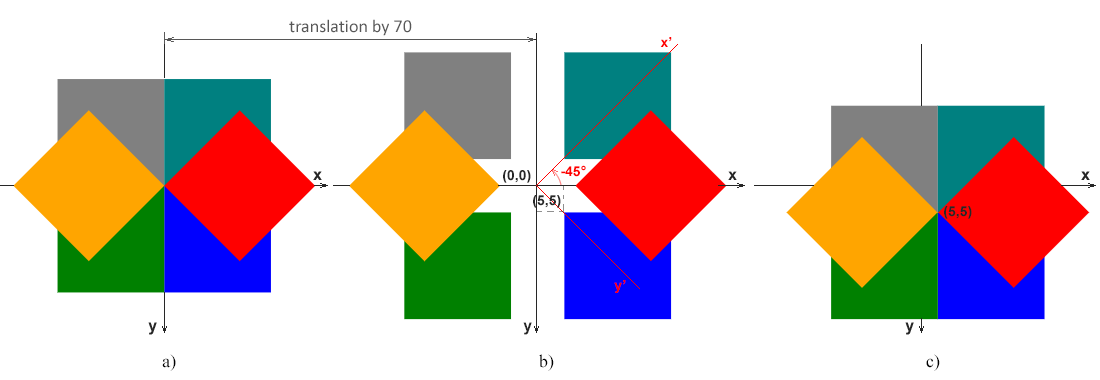
Sur fig. a montre le cas où le coin supérieur gauche du rectangle bleu (initial) (0, 0) correspond au point d’origine du système de coordonnées (0, 0).
Sur fig. b illustre le cas où le coin supérieur gauche du rectangle bleu (initial) (5, 5) ne correspond pas au point d’origine (0, 0). Cette figure montre les axes x-y du système de coordonnées d’origine, qui sont valables pour toutes les figures a, b et c. De plus, les axes x’-y’ du système de coordonnées du rectangle rouge, qui pivote de 45 degrés dans le sens inverse des aiguilles d’une montre α=-45°, sont affichés en rouge. Cela montre clairement que la rotation du rectangle est réduite à la rotation du système de coordonnées.
Sur fig. c montre le cas où le coin supérieur gauche du rectangle bleu (initial) (5, 5) ne correspond pas au point initial du système de coordonnées (0, 0), mais la rotation se produit autour du point (5, 5).
Remarque : La matrice suivante fera pivoter l’objet autour du point pivot (cx, cy):
matrix(cos(α), sin(α), -sin(α), cos(α), cx·(1-cos(α))+cy·sin(α), cy·(1-cos (α))-cx·sin(α))
Les coefficients cx·(1-cos(α))+cy·sin(α) et cy·(1-cos(α))-cx·sin(α) gèrent la translation nécessaire pour garantir que l’objet reste dans sa position d’origine après la rotation. Calculons ces valeurs pour le rectangle rouge (fig. c). Le point pivot (cx, cy) dans cet exemple est (5, 5) – le coin supérieur gauche du rectangle bleu (initial), et l’angle du rectangle rouge est de -45°:
cos(-45°)=0,7071, sin(-45°)=-0,7071
cx·(1-cos(α))+cy·sin(α)=5·(1-0,7071)+5·(-0,7071)=-2
cy·(1-cos(α))-cx·sin(α)=5·(1-0,7071)-5·(-0,7071)=5
Vous pouvez faire pivoter SVG en C# à l’aide d’Aspose.SVG pour l’API .NET. L’article
Faire pivoter SVG – Exemples C# couvre des exemples C# pour la rotation SVG. Des cas d’utilisation de la fonction rotate() dans l’attribut transform et de la matrice de transformation matrix(a,b,c,d,e,f) sont considérés.
Matrice d’inclinaison – Skewing Matrix
L’inclinaison est une transformation qui fait pivoter l’un des axes du système de coordonnées de l’élément d’un certain angle α dans le sens des aiguilles d’une montre ou dans le sens inverse. Les éléments SVG peuvent être asymétriques grâce à l’utilisation de la matrice d’inclinaison qui ressemble à ceci:
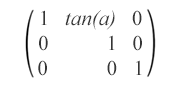
matrix(1,0,tan(α),1,0,0) – Cette matrice d’inclinaison spécifie une transformation d’inclinaison le long de l’axe des x de α degrés.
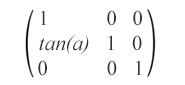
matrix(1,tan(α),0,1,0,0) – Cette matrice d’inclinaison spécifie une transformation d’inclinaison le long de l’axe y de α degrés.
Voici un exemple de cercle avec des transformations asymétriques:
1<svg viewBox="0 0 200 200" xmlns="http://www.w3.org/2000/svg">
2 <g fill="none">
3 <circle cx="20" cy="20" r="10" stroke="blue" />
4 <!-- skew transformation along the x-axis by α=45° -->
5 <circle cx="20" cy="20" r="10" stroke="red" transform="matrix(1,0,1,1,0,0)" />
6 </g>
7 <g fill="none" transform="translate(70)">
8 <circle cx="20" cy="20" r="10" stroke="blue" />
9 <!-- skew transformation along the y-axis by α=45° -->
10 <circle cx="20" cy="20" r="10" stroke="orange" transform="matrix(1,1,0,1,0,0)" />
11 </g>
12</svg>L’exemple rendu ressemble à:
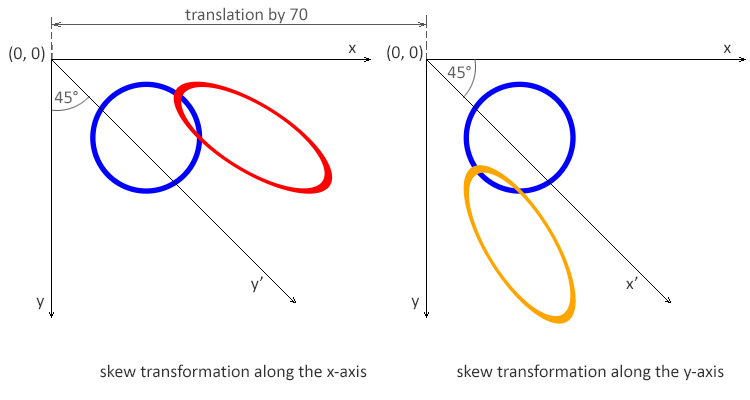
Remarque: La valeur d’angle α représente une transformation SVG inclinée en degrés le long de l’axe approprié. En utilisant la transformation d’inclinaison le long de l’axe des x, seule la coordonnée x des points de la forme change, mais la coordonnée y reste inchangée. La transformation d’inclinaison le long de l’axe des x donne l’impression que les lignes verticales ont été tournées d’un angle donné. La coordonnée x de chaque point change sur une valeur proportionnelle à l’angle spécifié et à la distance jusqu’à l’origine.
Conclusion
La matrice de transformation SVG est un outil puissant pour manipuler et animer des objets en SVG. Il offre un moyen polyvalent d’appliquer la translation, la rotation, la mise à l’échelle et l’inclinaison aux formes et aux éléments, vous permettant de créer des graphiques visuellement dynamiques et interactifs. La matrice permet des transformations individuelles et combinées, offrant la flexibilité nécessaire pour obtenir des effets visuels complexes et complexes. Nous n’avons couvert que les transformations individuelles dans cet article, mais nous essaierons bientôt d’élargir notre guide de dessin SVG avec de nouveaux articles avec des exemples plus complexes.
- Pour en savoir plus et obtenir des exemples de code SVG pour la rotation, la mise à l’échelle, le déplacement et l’inclinaison des graphiques SVG à l’aide de l’attribut de transformation SVG, veuillez consulter l’article
Transformations SVG.
- Lisez l’article
Transformations SVG – Exemples C# pour obtenir des exemples de code C# permettant de faire pivoter, mettre à l’échelle, traduire et incliner des graphiques SVG à l’aide d’Aspose.SVG pour la bibliothèque .NET.
- Aspose.SVG propose des Applications Web gratuites SVG pour convertir des fichiers SVG ou image, fusionner des fichiers SVG, vectoriser des images, générer des sprites SVG, encoder des données SVG en base64, et bien plus encore. Ces applications en ligne fonctionnent sur n’importe quel système d’exploitation doté d’un navigateur Web et ne nécessitent pas d’installation de logiciel supplémentaire. C’est un moyen rapide et simple de résoudre efficacement vos tâches liées au SVG!